特征工程学习笔记

2018-05-16

特征工程学习笔记

Fire 2018.5

1.探索性数据分析（EDA，Exploratory Data Analysis）

画图：

• matplotlib
• seaboan

2.数据预处理

2.1.1 基础方法

• 数据清洗
  1. 去重
  2. 过滤（把过高/过低的反常值用平滑值替代）
• 缺失值处理
  1. 直接赋0/-1
  2. 根据经验直接赋值
  3. 用已有的均值/中位数等统计值
  4. 用一个单独的机器学习算法通过其他特征来预测缺失值

  LightGBM和XGBoost都能将NaN作为数据的一部分进行学习，所以不需要处理缺失值。

• 二值化

  特征的二值化处理是将数值型数据输出为布尔类型。其核心在于设定一个阈值，当样本书籍大于该阈值时，输出为1，小于等于该阈值时输出为0。我们通常使用preproccessing库的Binarizer类对数据进行二值化处理。

• 标准化 标准化与归一化
  1. 均值方差法
  2. z-score标准化
  3. StandardScaler标准化

  把数据放缩到同样的范围 SVM/NN影响很大 树模型影响小。不是什么时候都需要标准化，比如物理意义非常明确的经纬度，如果标准化，其本身的意义就会丢失。

• 归一化
  1. 最大最小归一化（最常用）
  2. 对数函数转换（log）
  3. 反余切转换
• 区间缩放
  1. sklearn.preprocessing.MaxAbsScaler - scikit-learn 0.18.1 documentation，将一列的数值，除以这一列的最大绝对值。不免疫outlier。
  2. sklearn.preprocessing.MinMaxScaler - scikit-learn 0.18.1 documentation。不免疫outlier。
• 离散化
  1. one-hot
  2. 把数据按不同区间划分（等宽划分或等频划分）
  3. 聚类编码/按层次进行编码
  4. 平均数编码（mean encoding）：针对高基数类别特征的有监督编码。当一个类别特征列包括了极多不同类别时（如家庭地址，动辄上万）时，可以采用。
  5. 低频类别：有时会有一些类别，在训练集和测试集中总共只出现一次，例如特别偏僻的郊区地址。此时，保留其原有的自然数编码意义不大，不如将所有频数为1的类别合并到同一个新的类别下。
  6. hash编码成词向量

• 统计值

  包括max, min, mean, std等。python中用pandas库序列化数据后，可以得到数据的统计值。

• 压缩范围

  有些分类变量的少部分取值可能占据了90%的case，这种情况下可以采用预测模型、领域专家、或者简单的频率分布统计。具体问题具体分析，高频和低频都是需要特别处理的地方，抛弃效果不好时，可以考虑采样（高频）或上采样（低频），加权等等方法。

2.1.2 实例

• 不平衡类别
  1. 集成学习+阈值调整
  2. 多的类别过采样/少的类别欠采样来平衡分布欠采样（undersampling）和过采样（oversampling）会对模型带来怎样的影响？
• 时间特征
  1. 提取成年/月/日
  2. 根据活动按周期提取（每月/周）
  3. 尝试模型ARMA/RNN（脸书开源工具FBprofit）。
  4. 这是一年的第n天，这是一年的第n周，这是一周的第n天，etc
  5. 时间序列：把昨天的特征加入今天的特征，或者把和昨天相比，特征数值的改变量加入今天的特征。

3.特征构造

• 特征提取
  1. 相关领域专家知识（比如速度与加速度，时域（均值方差等）与频域（傅立叶变换）等）
  2. 深度学习自动学习特征
  3. 原始数据本身就是特征
  4. 实验/经验/发现
  5. 特征组合：如对用户id和用户特征最组合来获得较大的特征集
• 特征变换（普通加减乘除没有意义。）
  1. 不同阶的差分
  2. 傅立叶变换
  3. 多项式做组合特征（二次三次等）（sklearn.preprocessing.PolynomialFeatures - scikit-learn 0.18.1 documentation）对于树类模型没有多少意义
  4. 核方法

  5. 非正态分布转正太分布（log），平方，立方，根号…（但任何针对单独特征列的单调变换（如对数）：不适用于决策树类算法。对于决策树而言，X 、X^3 、X^5 之间没有差异，

     X

     、 X^2 、 X^4 之间没有差异，除非发生了舍入误差。）

  6. 线性组合（linear combination）：仅适用于决策树以及基于决策树的ensemble（如gradient boosting, random forest），因为常见的axis-aligned split function不擅长捕获不同特征之间的相关性；不适用于SVM、线性回归、神经网络等。
  7. 比例特征（ratio feature）：X_1 / X_2
  8. 绝对值（absolute value）
  9. max(X_1, X_2)，min(X_1, X_2)，X_1 xor X_2

  10. 类别特征与数值特征的组合：用N1和N2表示数值特征，用C1和C2表示类别特征，利用pandas的groupby操作，可以创造出以下几种有意义的新特征：（其中，C2还可以是离散化了的N1）

      median(N1)_by(C1) \ 中位数

      mean(N1)_by(C1) \ 算术平均数

      mode(N1)_by(C1) \ 众数

      min(N1)_by(C1) \ 最小值

      max(N1)_by(C1) \ 最大值

      std(N1)_by(C1) \ 标准差

      var(N1)_by(C1) \ 方差

      freq(C2)_by(C1) \ 频数

      freq(C1) \这个不需要groupby也有意义

      仅仅将已有的类别和数值特征进行以上的有效组合，就能够大量增加优秀的可用特征。

      将这种方法和线性组合等基础特征工程方法结合（仅用于决策树），可以得到更多有意义的特征，如：

      N1 - median(N1)_by(C1)

      N1 - mean(N1)_by(C1)

  11. 用基因编程创造新特征 Welcome to gplearn’s documentation!

    基于genetic programming的symbolic regression，具体的原理和实现参见文档。目前，python环境下最好用的基因编程库为gplearn。基因编程的两大用法：
    * 转换（transformation）：把已有的特征进行组合转换，组合的方式（一元、二元、多元算子）可以由用户自行定义，也可以使用库中自带的函数（如加减乘除、min、max、三角函数、指数、对数）。组合的目的，是创造出和目标y值最“相关”的新特征。这种相关程度可以用spearman或者pearson的相关系数进行测量。spearman多用于决策树（免疫单特征单调变换），pearson多用于线性回归等其他算法。
    * 回归（regression）：原理同上，只不过直接用于回归而已。
  

  1. 用决策树创造新特征

     在决策树系列的算法中（单棵决策树、gbdt、随机森林），每一个样本都会被映射到决策树的一片叶子上。因此，我们可以把样本经过每一棵决策树映射后的index（自然数）或one-hot-vector（哑编码得到的稀疏矢量）作为一项新的特征，加入到模型中。 具体实现：apply()以及decision_path()方法，在scikit-learn和xgboost里都可以用。

  2. Histogram映射：

     把每一列的特征拿出来，根据target内容做统计，把target中的每个内容对应的百分比填到对应的向量的位置。优点是把两个特征联系起来。

     例如我们来统计“性别与爱好的关系”，性别有“男”“女”，爱好有三种，表示成向量[散步、足球、看电视剧]，分别计算男性和女性中每个爱好的比例得到：男[1/3, 2/3, 0]，女[0, 1/3, 2/3]。即反映了两个特征的关系。

  3. 特征交叉

     特征交叉对于线性模型可以学习到非线性特征。例如两个特征：年龄和性别，可以组合成 年龄_性别 的一个新特征，比如M_18，F_22等等，然后再对这个特征做one hot编码，即可得到新的特征属性值。至于交叉特征的新特征向量是不是原特征向量的内积，答案是否。因为原特征也是one hot的离散变量，长度不一定相等，如果做向量内积是0。所以正确的做法是，先用原语义做简单字符串拼接，然后再做onehot编码。不过，暴力做交叉特征可能产生的稀疏的问题，这就是另一个问题了。可以参考FM和FFM的解决方案，LIBFFM的库，以及阿里妈妈发布的MLR算法。

• 特征升维
  1. 核方法
  2. autoencoder
  3. （CNN）多层神经网络编码

但是，并不是特征构造越多就效果越好。参见维度灾难。分类效果一开始会随着特征数量增加而提升，但到达顶峰后便会一直下降。有两个原因：

1. 特征越多，越容易过拟合；
2. 特征越多，数据越稀疏，需要相应增加的训练数据成指数级增长。

且在高维空间数据都分布在边角，中间几乎没有数据。因此，在高维空间用距离来衡量样本相似性的方法已经渐渐失效。

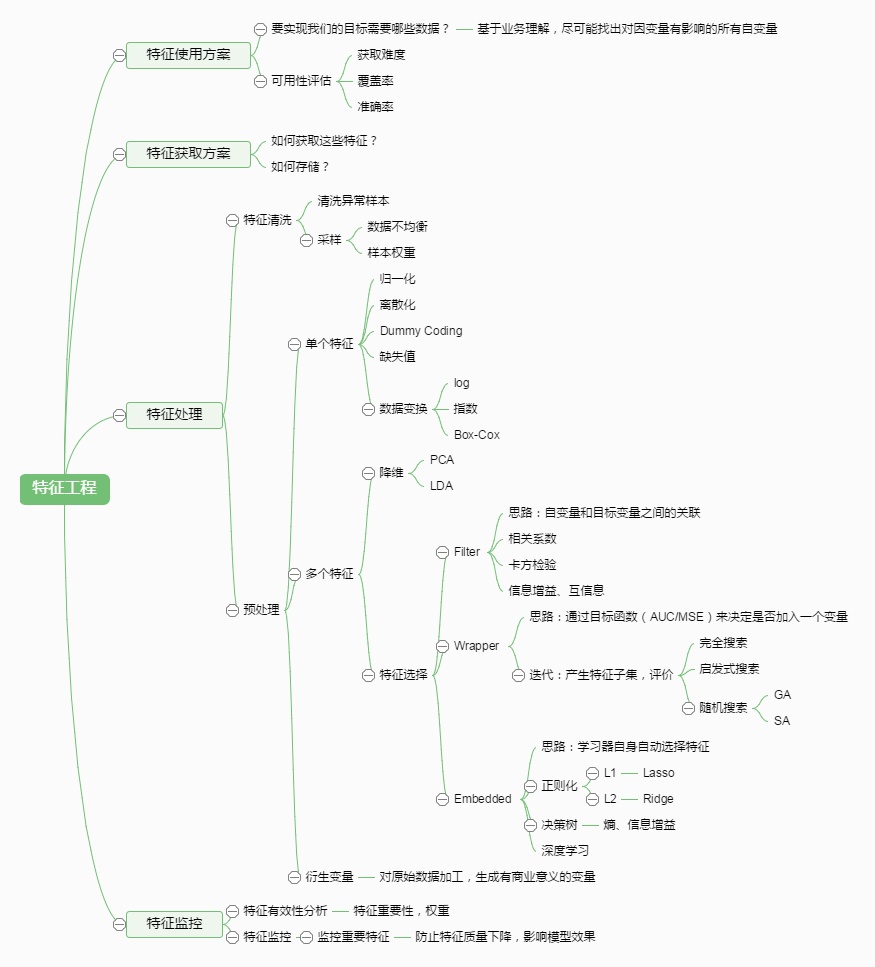
4.特征选择

特征选择的的一般流程就是， 找一个集合，然后针对某个学习算法， 测试效果如何， 一直循环直到找到最优集合为止。但时间花费很大。

一般需要考虑两点：

1. 特征是否发散：如果一个特征不发散，就是说这个特征大家都有或者非常相似，说明这个特征不需要。
2. 特征和目标是否相关：与目标的相关性越高，越应该优先选择。

按照特征评价标准分类：

• 选择使分类器的错误概率最小的特征或者特征组合。
• 利用距离来度量样本之间相似度。
• 利用具有最小不确定性（Shannon熵、Renyi熵和条件熵）的那些特征来分类。
• 利用相关系数, 找出特征和类之间存在的相互关系；
• 利用特征之间的依赖关系, 来表示特征的冗余性加以去除。

4.1特征选择 特征选择， 经典三刀

1. 过滤法Filter
   • 方差选择法:计算各个特征方差，选择方差大于阈值的特征 (Analysis of Variance：ANOVA,方差分析，通过分析研究不同来源的变异对总变异的贡献大小，从而确定可控因素对研究结果影响力的大小)。

   • 相关系数法:计算各个特征的Pearson相关系数

     皮尔逊系数只能衡量线性相关性而互信息系数能够很好地度量各种相关性，但是计算相对复杂一些，好在很多toolkit里边都包含了这个工具（如sklearn的MINE），得到相关性之后就可以排序选择特征了 (皮尔逊相关系数，更多反应两个服从正态分布的随机变量的相关性，取值范围在 [-1,+1] 之间。)

   • 互信息法:计算各个特征的信息增益
   • Linear Discriminant Analysis(LDA，线性判别分析)：更 像一种特征抽取方式，基本思想是将高维的特征影到最佳鉴别矢量空间，这样就可以抽取分类信息和达到压缩特征空间维数的效果。投影后的样本在子空间有最大可分离性。
   • Chi-Square：卡方检验，就是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，卡方值越大，越不符合；卡方值越小，偏差越小，越趋于符合。

   优点： 快速， 只需要基础统计知识。缺点：特征之间的组合效应难以挖掘。

2. 封装法Wrapper
   • 递归消除法:使用基模型(如LR)在训练中进行迭代，选择不同 特征
   • 构建单个特征的模型，通过模型的准确性为特征排序，借此来选择特征
   • 前向选择法：从0开始不断向模型加能最大限度提升模型效果的特征数据用以训练，直到任何训练数据都无法提升模型表现。
   • 后向剃除法：先用所有特征数据进行建模，再逐一丢弃贡献最低的特征来提升模型效果，直到模型效果收敛。

   优点： 直接面向算法优化， 不需要太多知识。缺点： 庞大的搜索空间， 需要定义启发式策略。

3. 嵌入法Embedded(效果最好速度最快，模式单调，快速并且效果明显， 但是如何参数设置， 需要深厚的背景知识。)

   • 使用带惩罚项的基模型进行特征选择

     比如LR加入正则。通过L1正则项来选择特征：L1正则方法具有稀疏解的特性，因此天然具备特征选择的特性，但是要注意，L1没有选到的特征不代表不重要，原因是两个具有高相关性的特征可能只保留了一个，如果要确定哪个特征重要应再通过L2正则方法交叉检验

   • 树模型的特征选择(随机森林、决策树)

     训练能够对特征打分的预选模型：RandomForest和Logistic Regression等都能对模型的特征打分，通过打分获得相关性后再训练最终模型；

   • Lasso
   • Elastic Net
   • Ridge Regression

   优点： 快速， 并且面向算法。缺点： 需要调整结构和参数配置， 而这需要深入的知识和经验。

此外还可以通过深度学习来进行特征选择：目前这种手段正在随着深度学习的流行而成为一种手段，尤其是在计算机视觉领域，原因是深度学习具有自动学习特征的能力，这也是深度学习又叫unsupervised feature learning的原因。从深度学习模型中选择某一神经层的特征后就可以用来进行最终目标模型的训练了。

4.2 特征降维

特征选择是在原本特征集合中取一部分出来，是特征集合的子集，特征降维做特征的计算组合后构成新特征。

1. 线性降维
   • 主成分分析(PCA):选择方差最大的K个特征[无监督]
   • 线性判别分析(LDA):选择分类性能最好的特征[有监督]
2. 非线性降维（大多是流行学习）
   • 核主成分分析(KPCA):带核函数的PCA
   • 局部线性嵌入(LLE):利用流形结构进行降维
   • 还有拉普拉斯图、MDS等
3. 迁移成分分析(TCA):不同领域之间迁移学习降维
   • 使用带惩罚项的基模型进行特征选择(比如LR加入正则)
   • 树模型的特征选择(随机森林、决策树)

• 人肉：SIFT, VLAD, HOG, GIST, LBP
• 模型：Sparse Coding, Auto Encoders, Restricted Boltzmann Machines, PCA, ICA, K-means

工具：Scikit-learn，可以特征选择、降维

参考资料

• 知乎live机器学习入门之特征工程——王晋东
• 知乎特征工程话题下部分答案